Computing with encrypted data
by Brian Hayes
Published 16 August 2012
Let’s suppose you are a client of the notorious accounting firm Dewey, Cheetham & Howe. You want them to compute your income tax, but you don’t trust them with the confidential details of your financial life. 
This impasse seems insurmountable. Surely there is no way for an accountant to calculate your income tax without knowing your income. More generally, you can’t apply an algorithm to data unless you have access to the data.
Or so you might think. Consider the computing scheme known as fully homomorphic encryption. With this protocol you encrypt your data and send the ciphertext off to the untrustworthy accountants, who cannot decrypt it or otherwise learn anything about its content. Nevertheless, they can perform computations on the data, producing results that are also encrypted. When they send back the output of the computation, you apply your private decryption key, getting the same answers you would have obtained if the entire operation had been conducted in the open. In my opinion this is one of the most amazing magic tricks in all of computer science.
If you’d like to learn more about homomorphic encryption, I can recommend a place to start: my column in the new issue of American Scientist. Get it now in HTML or PDF.
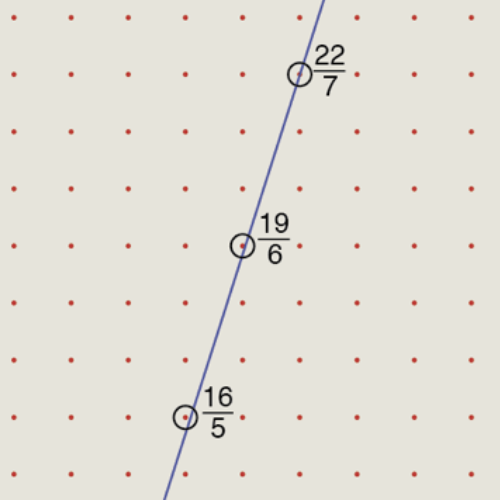
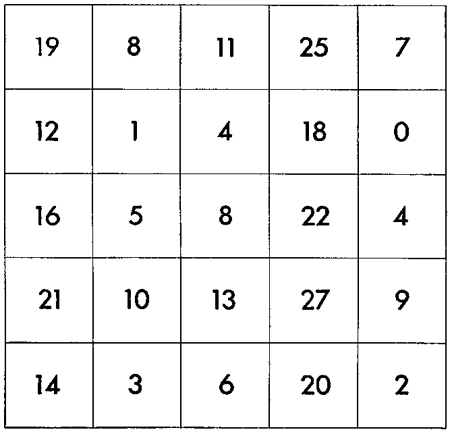
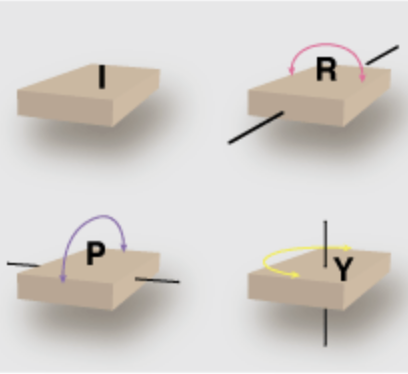
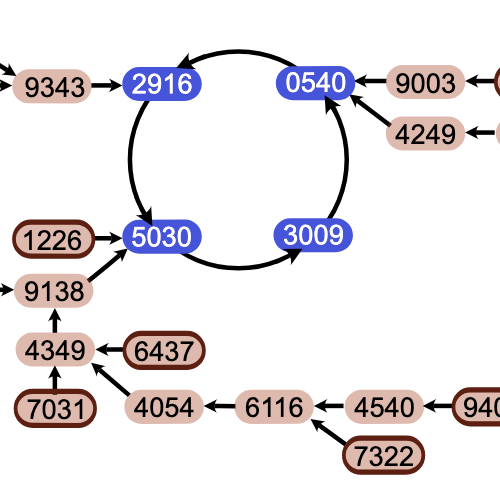
One further note about the column: For crypto buffs, there’s an Easter egg in the first illustration.
Responses from readers:
Please note: The bit-player website is no longer equipped to accept and publish comments from readers, but the author is still eager to hear from you. Send comments, criticism, compliments, or corrections to brian@bit-player.org.
Publication history
First publication: 16 August 2012
Converted to Eleventy framework: 22 April 2025
I imagine audits would be problematic. Or maybe there’s such a thing as a homomorphic audit? Seems a tad opaque to satisfy the purpose of an audit though.
A perfect choice for an Easter egg.